Aula 05 – Conceitos fundamentais de estatística descritiva – Medidas de dispersão – Ciência de Dados Aplicada ao Direito, Sistemas de Informação Jurídicos e Gestão de Serviços Jurídicos

Leitura e links para a aula:

Planilha do Google Spreadsheets com dados de idade dos alunos

Introdução

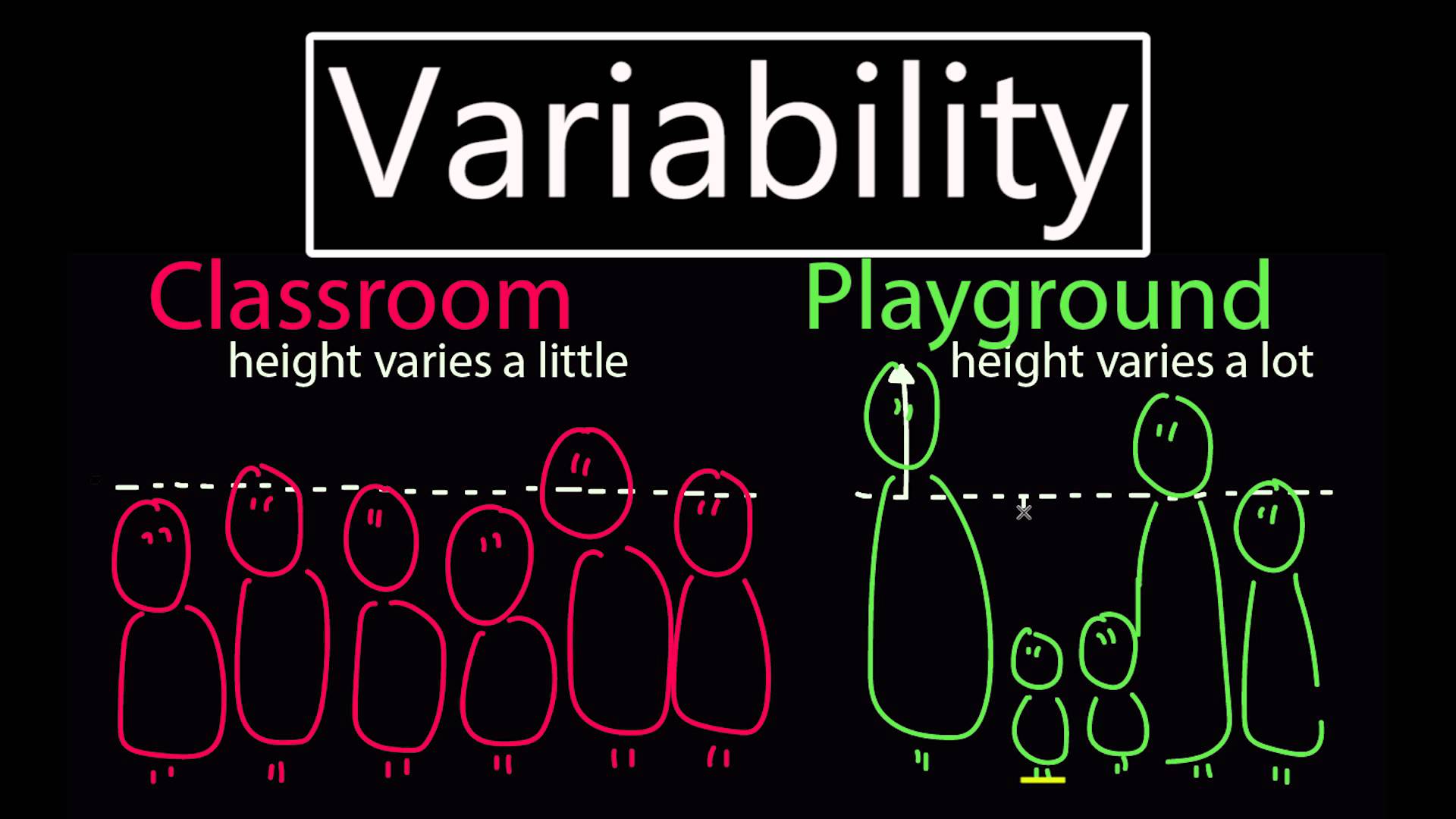
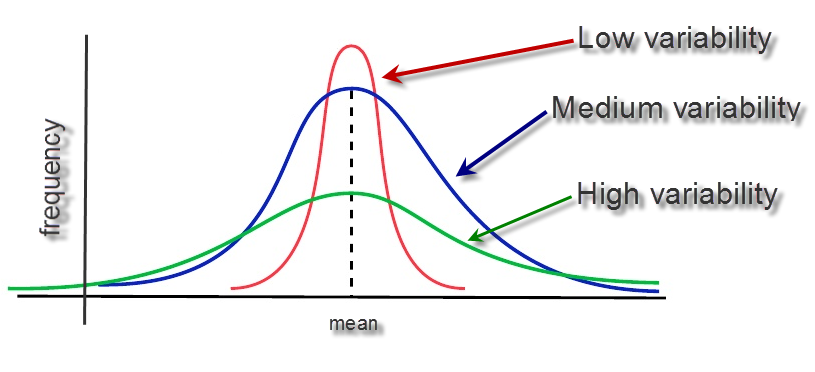
Um conjunto de dados pode ser caracterizado, além do uso das medidas de tendência central ou de elemento típico, pela dispersão ou variabilidade dos dados. Didaticamente, podemos pensar que dois conjuntos de dados que possui a mesma média podem ser completamente diferentes: um mais “espalhado” outro mais “concentrado”.

Visão intuitiva de variabilidade. Dois conjuntos de dados possuem a mesma média, mas as alturas são muito mais uniformes na mesma sala e divergentes no pátio do colégio.

Exemplos de conjuntos de dados que possuem a mesma média mas variabilidades completamente diferentes.

Amplitude Total

A amplitude total é a medida mais simples de “espalhamento” dos dados. Ela é a distância entre o maior e o menor elementos do conjunto. Entretanto, trata-se de uma medida muito singela e grosseira.

AT = Max – Min

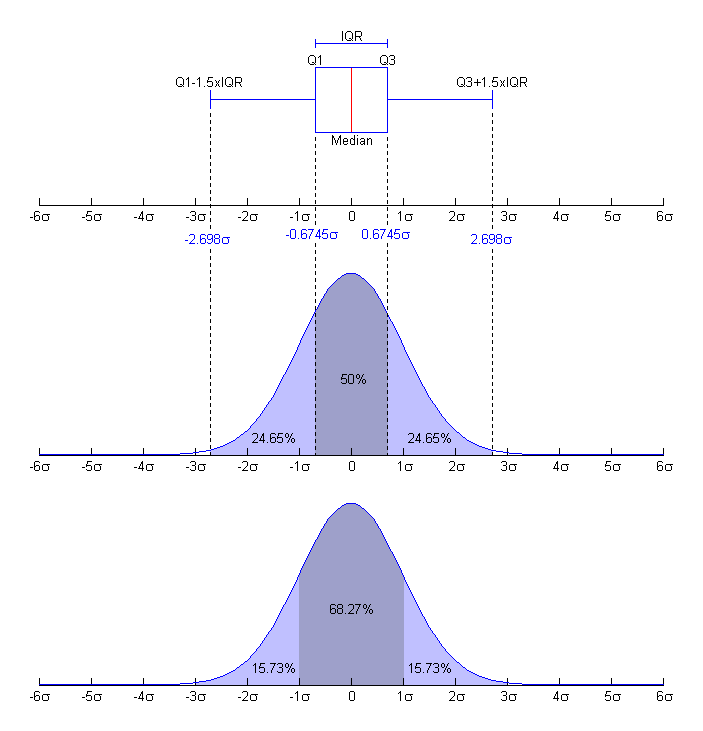
Amplitude ou Distância Interquartil

Distância interquartil para uma distribuição normal ou gaussiana.

Variância

A amplitude total e a distância interquartil padecem do mesmo problema: são medidas muito simples. Deveríamos usar uma medida que considerasse todos os elementos do conjunto de dados.

Tomemos novamente as idades dos alunos da sala, e usemos a distância de cada um desses elementos até o elemento típico (média). Lembremos que a média para o conjunto é 24,7 anos:

Idade	(xi – x)	(xi – x)2
18	-6,7	44,83
19	-5,7	32,44
19	-5,7	32,44
20	-4,7	22,05
20	-4,7	22,05
20	-4,7	22,05
20	-4,7	22,05
21	-3,7	13,66
21	-3,7	13,66
21	-3,7	13,66
21	-3,7	13,66
22	-2,7	7,27
22	-2,7	7,27
22	-2,7	7,27
22	-2,7	7,27
26	1,3	1,7
27	2,3	5,31
28	3,3	10,92
29	4,3	18,53
30	5,3	28,14
37	12,3	151,4
38	13,3	177,01
45	20,3	412,27
SOMA	0	1086,87

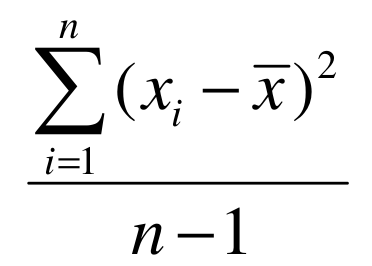
No exemplo acima, a variância, que é representada pela letra grega sigma ou pela latina s:

s = 1086,87 / 22 = 49,40

Desvio Padrão

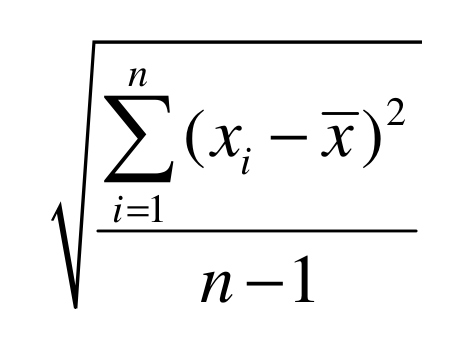
Entretanto, a medida da variância está em valores quadrados. O que significam 49,40 anos ao quadrado (ou quilos ao quadrado, ou dias ao quadrado?). O desvio padrão “retorna” a medida para a unidade original. No exemplo, o desvio padrão é de 7,02 anos.

Coeficiente de Variação

CV = S / X

Para o presente caso:

7,02 / 24,69 = 0,28