Conceitos fundamentais de estatística descritiva – Medidas de tendência central

/ Tópicos em Sociologia - Métodos Quantitativos nas Ciências Sociais / Por

Leitura e links para a aula:

Distribuição

Histograma de Idade
Boxplot de Idade
Histograma de Peso
Boxplot de Peso
Origem
Curso
Duração dos processos em dias
Boxplot de duração
Boxplots comparando a duração de processos físicos e digitais
Scatter Plot Expectativa x Renda

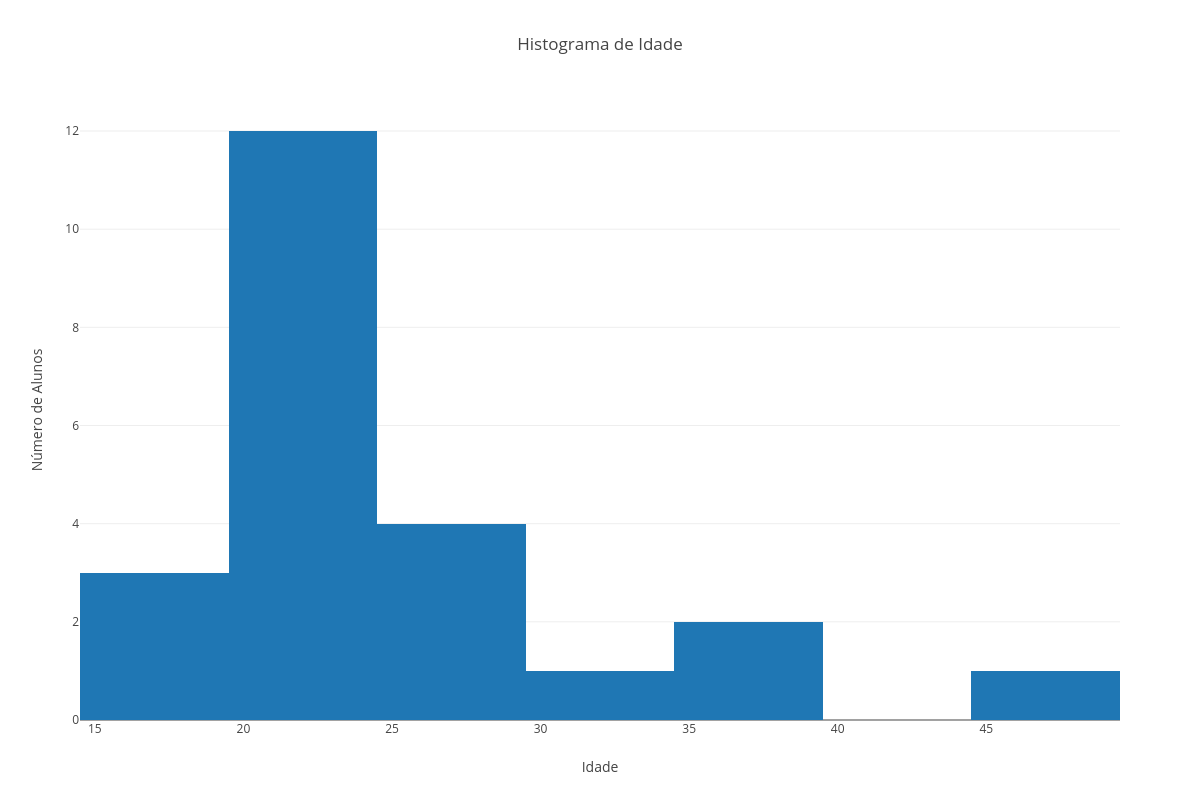
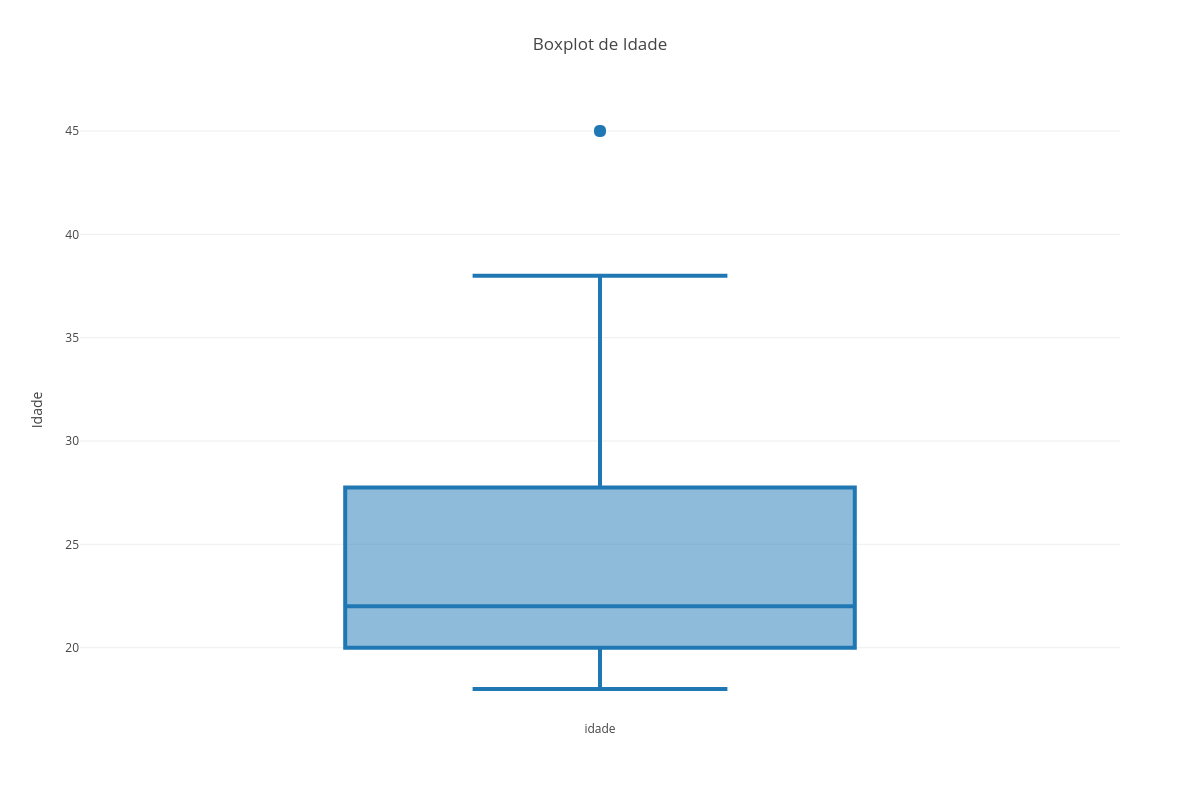
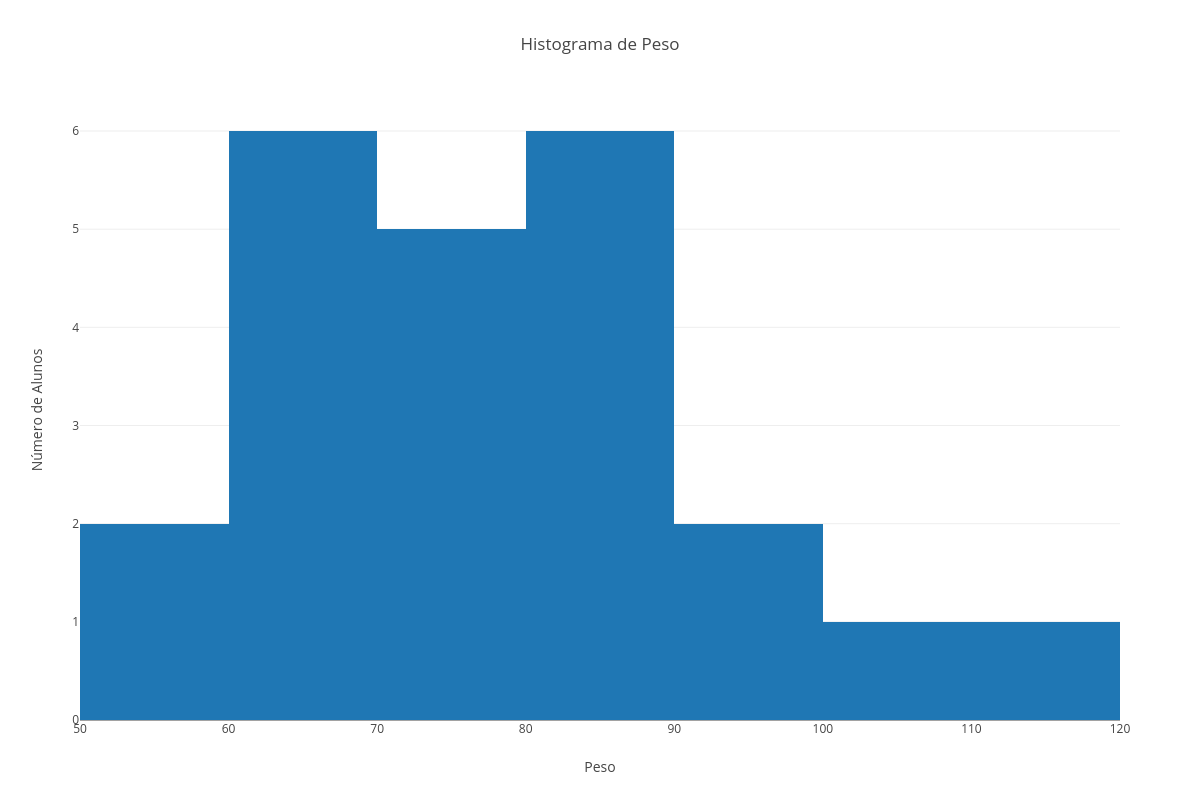
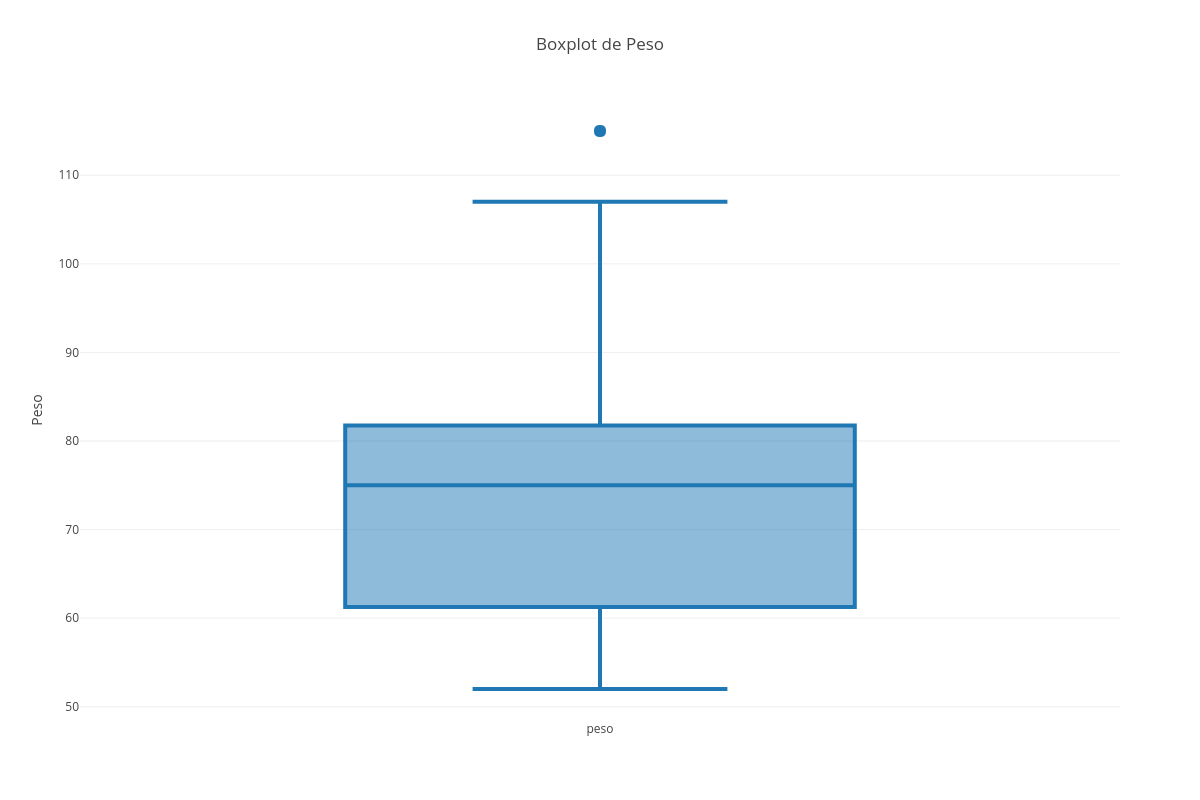
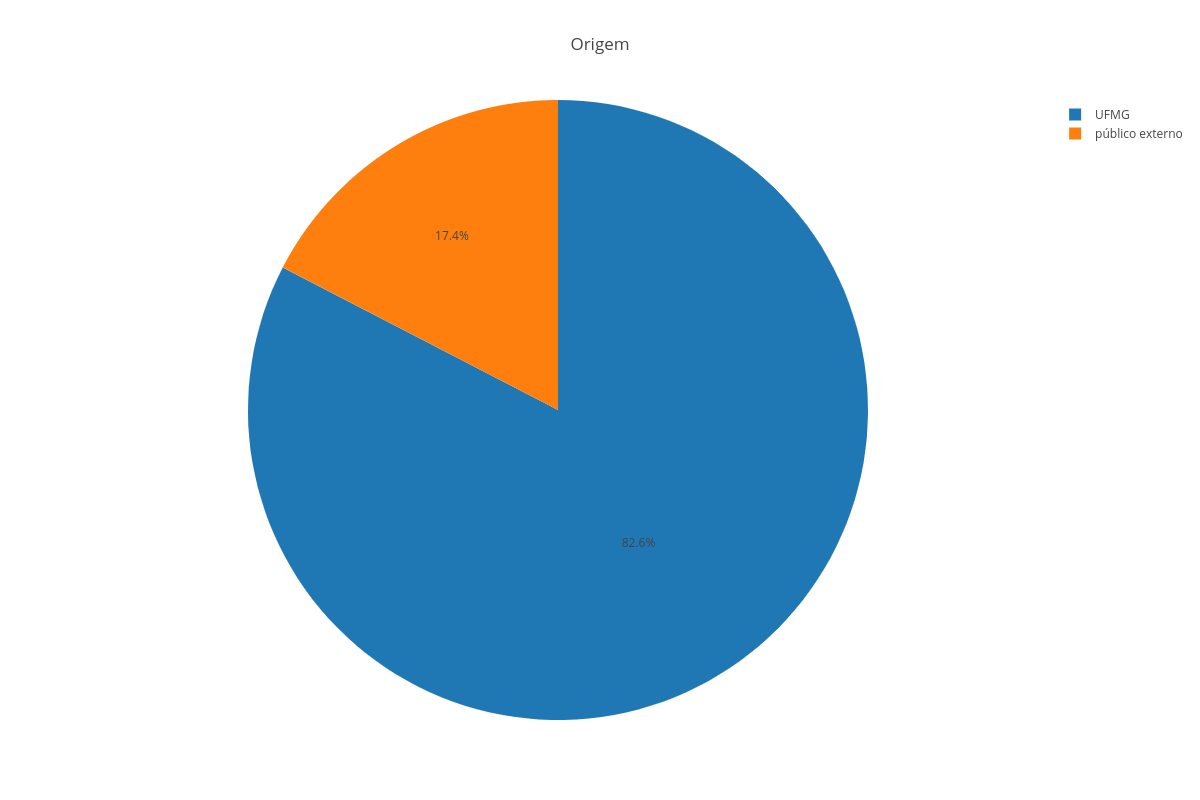
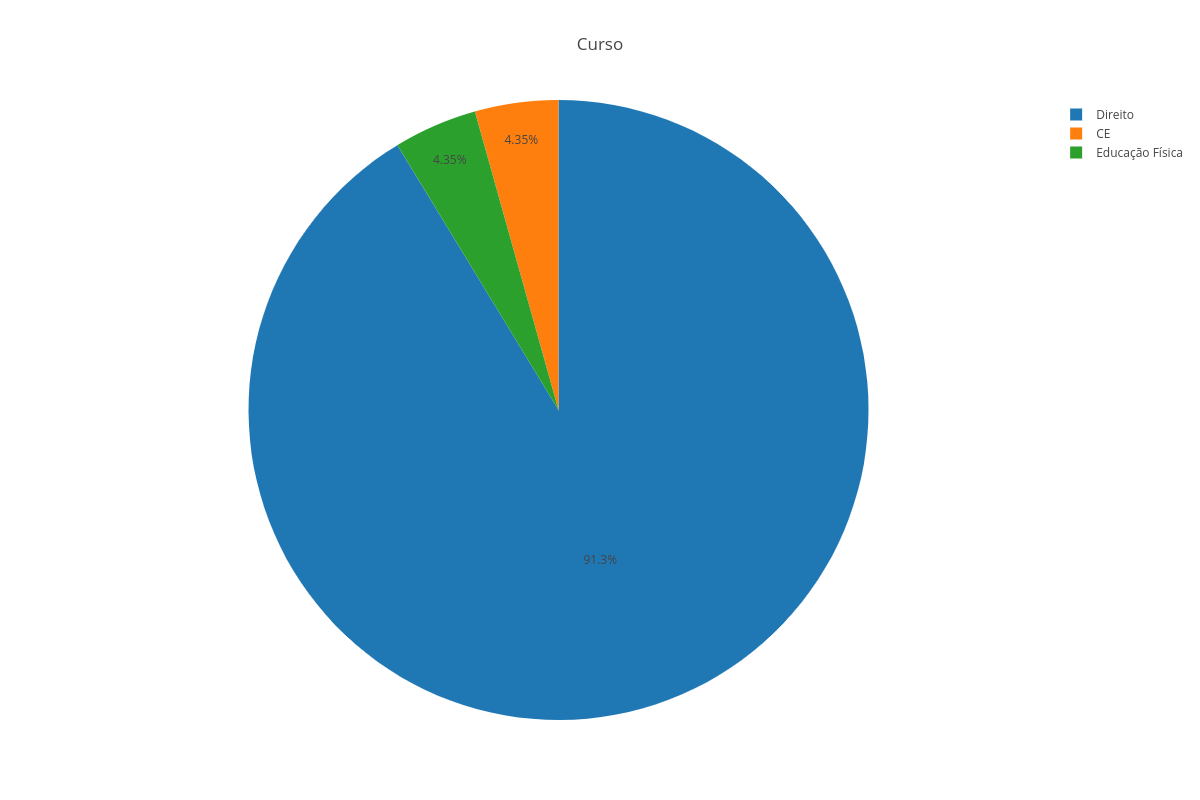
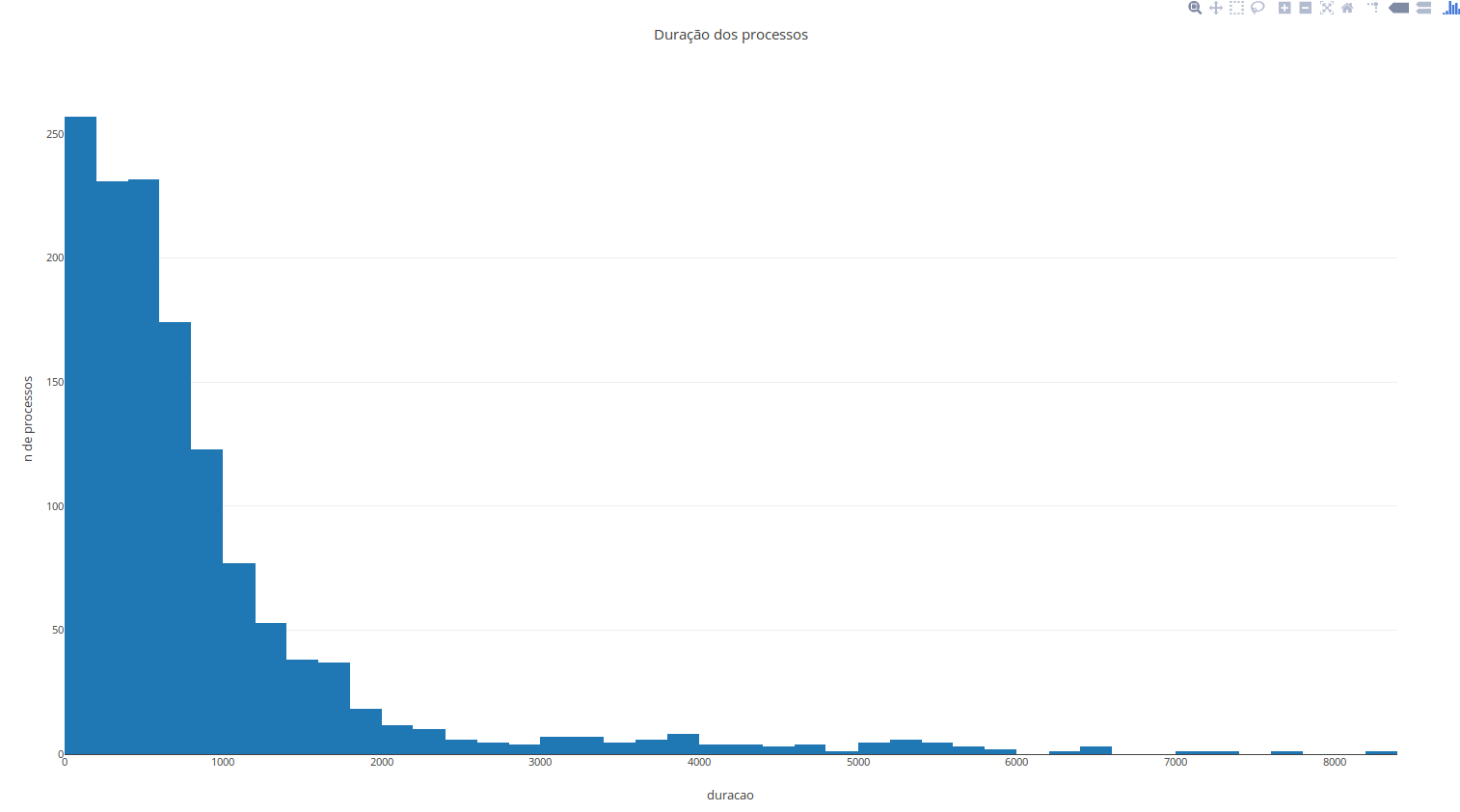
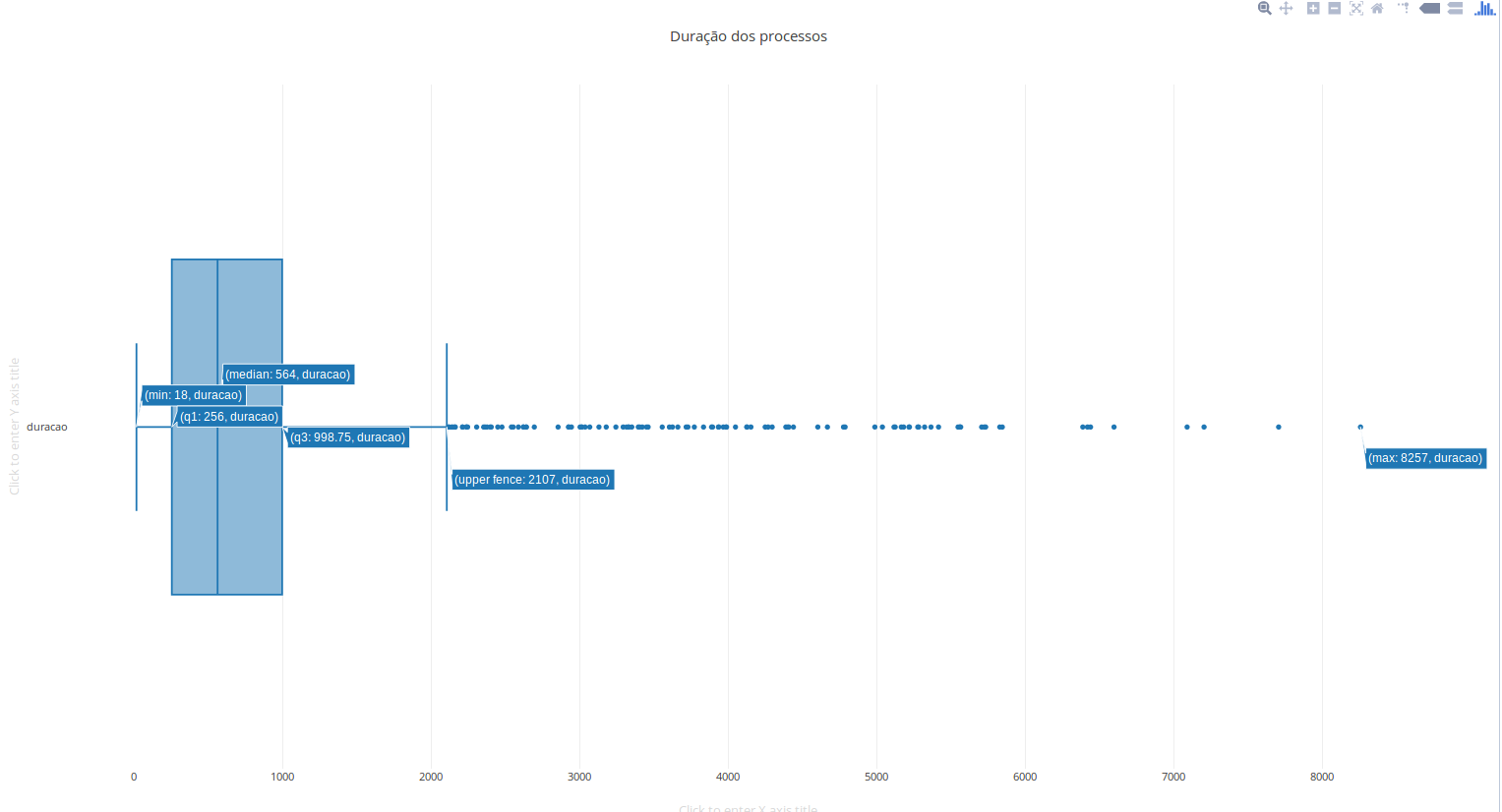
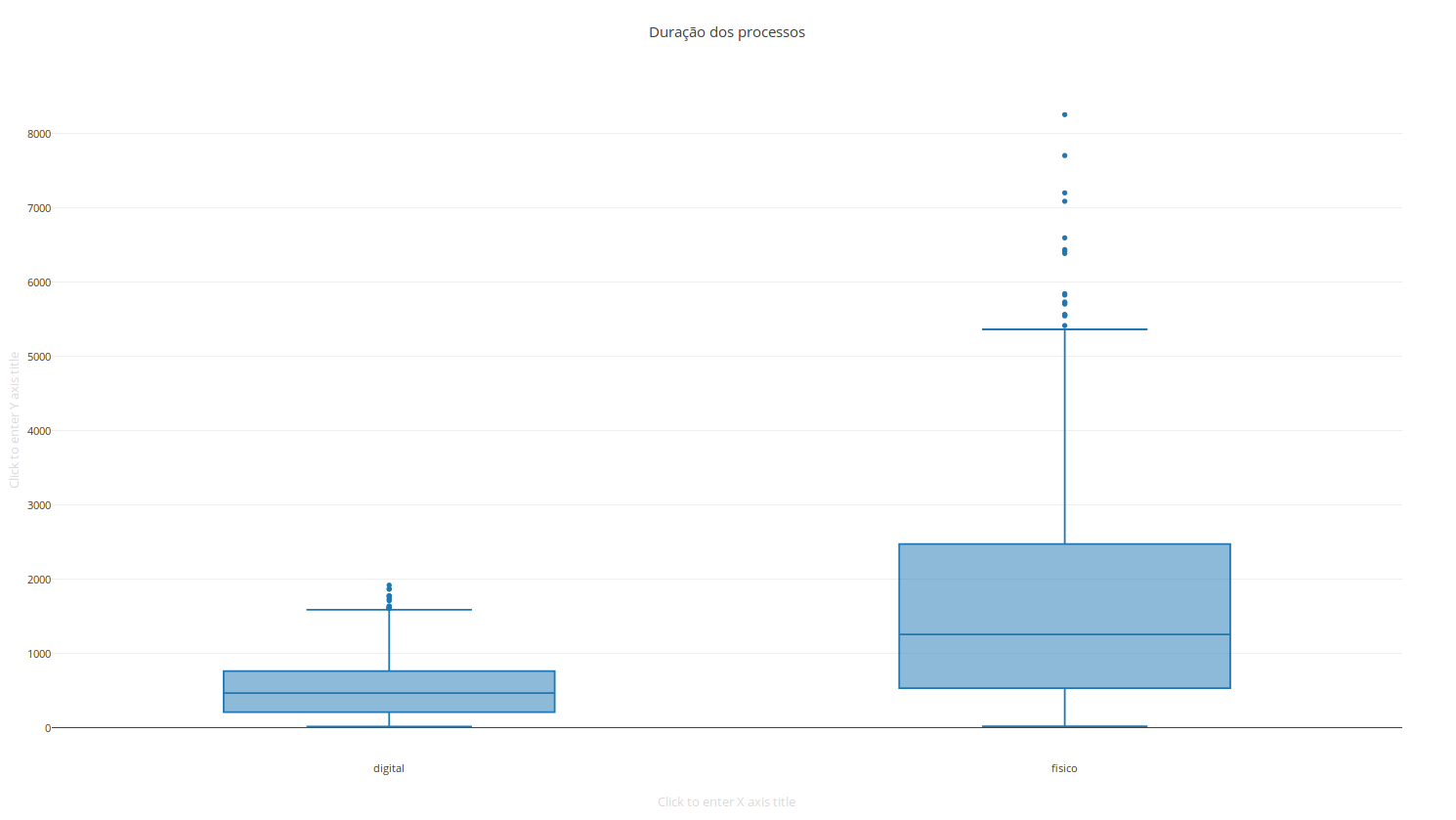
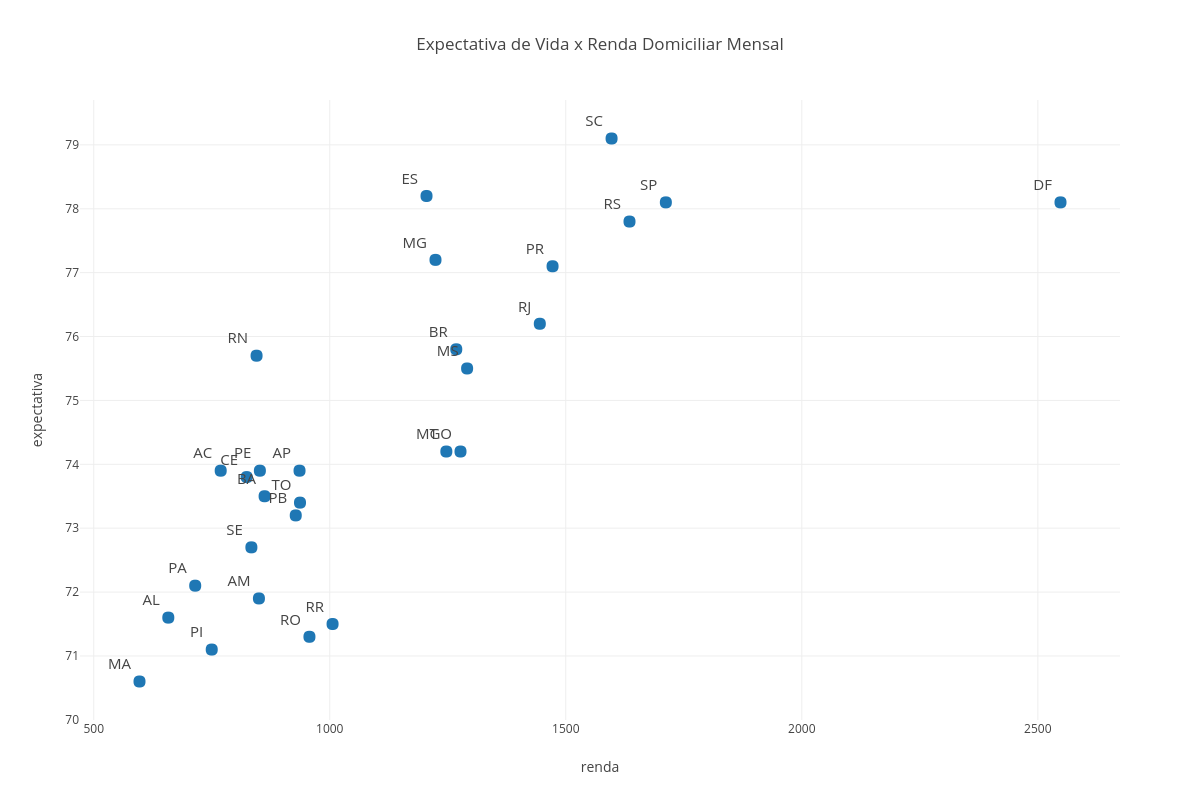
Dado o conjunto de dados: A = [1, 2, 3, 6, 6, 6, 7, 7, 9, 11, 12, 24, 55]

Média

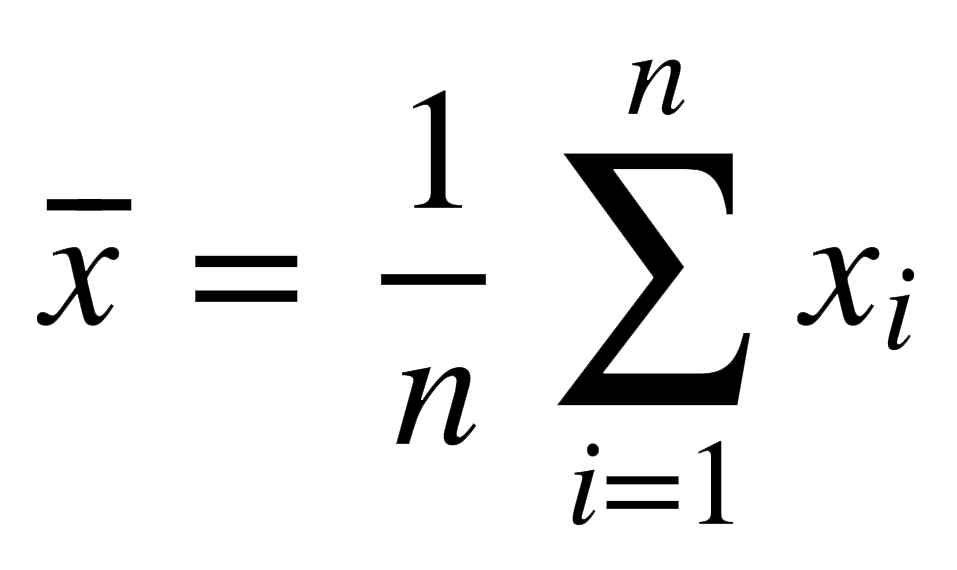
Fórmula para média aritmética. O x com uma barra representa a média da amostra. n o número de elementos do conjunto. O sigma representa o somatório. O i representa o índice do elemento, ou seja, sua posição na lista. Essa fórmula deve assim ser “interpretada”: some-se todos os elementos do conjunto, deo primeiro (i=1 embaixo do sigma) até o fim (n no topo). Depois, divida o resultado por n.

A média arimética de A:

Soma de todos os elementos de A:

1 + 2 + 3+ 6 + 6 + 6 + 7 +7 + 9 + 11 +12 + 24 + 55 = 149

Divisão da soma pelo número (13) de elementos de A.

149 / 13 = 11,46

Mediana

1, 2, 3, 6, 6, 6, 7, 7, 9, 11, 12, 24, 55

Como o n de itens em A é ímpar, a mediana é o item que parte o conjunto em dois: 7

Se o n fosse par, e.g., B = [1, 2, 3, 6, 6, 6, 7, 9, 11, 12, 24, 55]

A mediana seria a média dos dois elementos do meio: (6+7) / 2 = 6,5

Moda

A moda é simplesmente o item que mais se repete. No caso, 6.